Невозможно предсказать точно, куда упадет выпущенный из орудия снаряд: тут в ваши расчеты вмешивается случайность.
Зато, если вы выпустите из орудия, не изменяя наводки, много снарядов, произведете по цели, скажем, сотню выстрелов или больше, то тут вы уже сможете предсказать, как упадут снаряды.
Результаты случайных явлений, оказывается, тоже подчиняются некоторой количественной закономерности. Рассеивание снарядов только на первый взгляд происходит совершенно беспорядочно. На самом же деле результаты рассеивания подчиняются определенному закону.
Итак, предположим, что вы действительно произвели из орудия подряд сто выстрелов. Ваши снаряды упали где-то на расстоянии нескольких километров от орудия, разорвались и вырыли в земле сто воронок.
Как расположатся эти воронки?
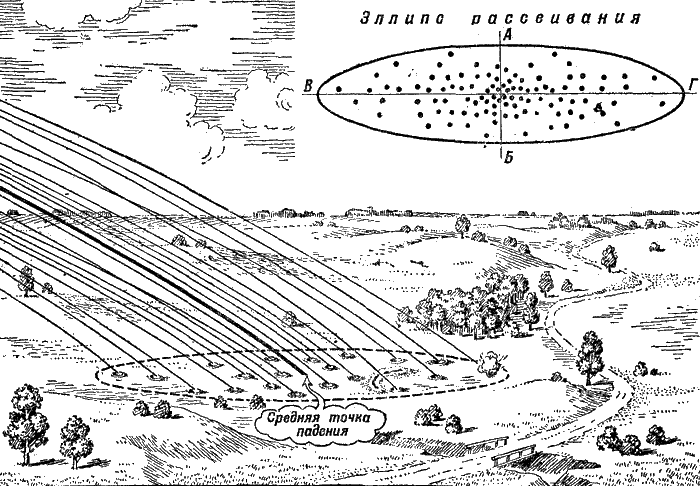
Прежде всего, участок, в котором заключаются воронки, образует некоторую геометрическую фигуру. Если вы очертите этот участок по всем крайним воронкам, то получите вытянутую в направлении стрельбы фигуру, похожую на эллипс (рис. 199). За границами этого эллипса воронок совсем не будет.
Но этого мало. Внутри эллипса воронки распределятся по некоторому, очень простому, правилу: чем ближе к центру эллипса, тем гуще, ближе одна от другой будут лежать воронки; чем дальше от центра, тем они будут лежать реже, а у самых краев эллипса их будет совсем мало.
Таким образом, в пределах площади рассеивания всегда будет такая точка, около которой окажется наибольшее число попаданий; точка эта совпадет с центром эллипса. Эта точка, около которой можно с наибольшей вероятностью ожидать падения снарядов, называется средней точкой падения (рис. 199). Ей соответствует средняя траектория снарядов, то-есть траектория, проходящая в середине снопа.
Если бы никакие случайности не вмешивались в стрельбу, то все снаряды полетели бы один за другим как раз по этой средней траектории и попали бы в самый центр эллипса.
Относительно средней точки падения все воронки будут группироваться, до известной степени, симметрично.
Если стать в том месте площади рассеивания, где наиболее густо расположились воронки, – в средней точке падения, – то можно заметить, что впереди этой точки упало снарядов примерно столько же, сколько и позади, а вправо примерно столько же, сколько и влево (рис. 199).
Таков закон рассеивания снарядов при стрельбе.
Без знания этого закона нельзя считать себя грамотным стрелком-артиллеристом.
Знание этого закона приносит артиллеристу большую пользу: оно подсказывает, сколько нужно выпустить снарядов по цели, чтобы рассчитывать на попадание.
Но чтобы извлечь из этого закона всю пользу, которая в нем таится, нужно его прежде всего сформулировать математически.
Сделать это совсем не трудно.
Для этого прежде всего проведите ось рассеивания по дальности (на рис. 199 линия АБ). Этой осью явится такая линия, перед которой и за которой число воронок будет одинаковым, то-есть по 50.
Рис. 199. Рассеивание снарядов; справа вверху – примерное распределение сотни воронок
Теперь отсчитайте 25 воронок, расположенных ближе других к оси рассеивания по одну ее сторону, и отделите эти воронки линией, параллельной оси рассеивания (рис.200). Ширина полученной вами полосы – очень важный показатель рассеивания; ее называют «срединным отклонением» по дальности. Действительно, если вы отложите такую же полосу по другую сторону оси рассеивания, то в двух этих полосах у вас будет заключена «лучшая» половина всех попаданий. Лучшая потому, что эти 50 попаданий легли густо около средней точки падения.
Рис. 200. Процентное распределение сотни воронок в эллипсе рассеивания
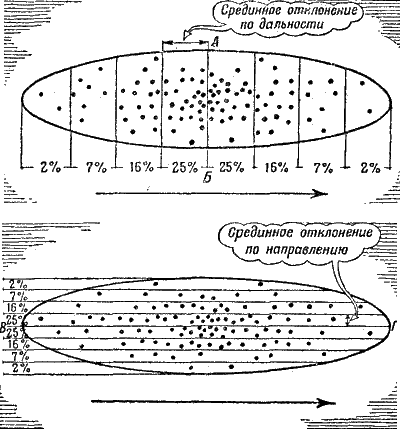
Если теперь вы будете дальше откладывать вперед и назад полосы, равные срединному отклонению, то можно будет установить математическое выражение закона рассеивания. Вы увидите, что таких полос получится у вас всего 8, по 4 в каждую сторону от оси рассеивания (рис. 200). И в каждой полосе окажется определенное число воронок, показанное на рисунке.
То же самое получится и в том случае, если вы проведете полосы не поперек, а вдоль эллипса (рис. 200).
25%, 16%, 7%, 2% – эти числа стоит запомнить, они вам пригодятся: ведь это и есть численное выражение закона рассеивания.
Из какого бы орудия вы ни стреляли, все равно попадания снарядов распределятся по этому закону.
Конечно, если вы произведете немного выстрелов, то вы получите, может быть, не совсем такие числа. Но чем больше выстрелов произведено, тем яснее будет проявляться закон рассеивания.
Закон этот действителен во всех случаях: стреляете ли вы по малой цели или по большой, далеко или близко, из такого орудия, которое очень сильно рассеивает снаряды, или из такого, которое рассеивает снаряды мало, – обладает, как говорят артиллеристы, большой «кучностью боя». Вся разница будет в том, что в одном случае у вас получится большой эллипс, а в другом – малый.
Чем больше эллипс, чем шире каждая из его восьми полос, тем, значит, рассеивание больше. Наоборот, чем эллипс меньше, чем каждая из его восьми полос уже, тем, значит, рассеивание меньше.
По срединному отклонению вы можете, таким образом, судить о величине рассеивания, о кучности боя орудия.
Из рисунков ясно видно, что срединное отклонение боковое всегда меньше, чем срединное отклонение по дальности. Это значит: всякое орудие больше рассеивает снаряды по дальности (вперед-назад), чем в стороны (вправо-влево).
Мы уже знаем, что траектории снарядов, если смотреть на них от орудия, имеют вид расходящегося снопа (рис. 198).
Ясно, что траектории разойдутся тем больше, – а в связи с этим и рассеивание будет тем больше, – чем на большую дальность мы стреляем.
Примерные размеры эллипсов рассеивания для двух наших орудий при стрельбе на разные дальности показаны на рисунке 201.
Рис. 201. Чем больше дальность стрельбы, тем больше и рассеивание. У гаубицы рассеивание снарядов по дальности меньше, чем у пушки
В бою всегда приходится помнить о рассеивании и считаться с ним.
Именно поэтому, прежде чем начать стрельбу по какой-нибудь цели, артиллерист должен продумать, сколько приблизительно понадобится снарядов, чтобы эту цель поразить, есть ли вообще смысл тратить на эту цель такое количество снарядов.
Цель маловажная – да еще малых размеров – не должна соблазнять артиллериста. Стрельба по такой цели приводит только к лишнему расходу снарядов и времени. А в бою очень дороги каждый снаряд и каждая минута.
Стрелять из артиллерийского орудия в боевой обстановке – это совсем не то, что стрелять из ружья в садовом тире, где много занимательных фигур – целей. В тире вы можете стрелять по любой цели. В бою же от артиллериста требуется не только умение стрелять, но еще и умение правильно выбирать цель.
Вот, например, какой-то всадник противника показался на дороге, удаленной на 5 километров от нашей дивизионной пушки. В бинокль его отлично видно на фоне неба. Вот он остановился, как будто изучает поле боя. Быть может, это крупный вражеский начальник? Имеет ли, однако, смысл открыть по этой цели огонь из пушки? Посмотрите на рисунок 201. На дальность в 5 километров наша пушка дает эллипс рассеивания длиной 232 метра и шириной 25 метров. Можно ли при этих условиях рассчитывать на попадание в отдельного всадника не только целым снарядом, но даже отдельным осколком или шрапнельной пулей? Очевидно, для этого понадобились бы очень много снарядов, и то без всякой уверенности в успехе стрельбы. А так как цель эта в данный момент ничем особо не вредит нашим войскам, стрельба по ней явно не имеет смысла – это была бы действительно «стрельба из пушки по воробьям».
Бессмысленность стрельбы по мелким, неважным удаленным целям – не единственный результат рассеивания. Бывают случаи, когда рассеивание причиняет крупные неприятности.
Вот, например, случай, когда наша и неприятельская пехота приходят в близкое соприкосновение друг с другом: тут уж рассеивание может послужить даже причиной «стрельбы по своим».
Когда цель находится недалеко от нашей пехоты, некоторые снаряды вследствие рассеивания могут не долететь до цели, упасть ближе, чем нужно, в наше расположение. Так, например, если наша артиллерия ведет стрельбу через нашу пехоту, примерно на 3-4 километра, то находиться ближе 200—250 метров от цели уже опасно. В этом случае наша пехота может быть поражена не только осколками (от них еще можно укрыться), но и целыми снарядами. Поэтому, как только наша пехота подойдет к цели ближе чем на 250 метров, артиллерия, стрелявшая через пехоту, сейчас же переносит огонь несколько дальше и предоставляет пехоте бороться с ближними целями своими средствами.
Поэтому-то, между прочим, пехота и имеет свою собственную артиллерию, которая передвигается вместе с пехотой и в такие моменты поражает важные ближние цели своим метким огнем.
Если же артиллерия стреляет не фронтальным, а фланговым огнем, то-есть с позиции, находящейся сбоку (рис. 202), то своя пехота может подойти к цели значительно ближе: в этом случае опасным является рассеивание снарядов только в стороны, а оно, как мы знаем, всегда значительно меньше, чем рассеивание в направлении стрельбы.
Рис. 202. Фланговый огонь по пехоте противника, расположенной вдоль фронта, выгоднее фронтального огня. Пунктиром обведены площади рассеивания снарядов; видны воронки
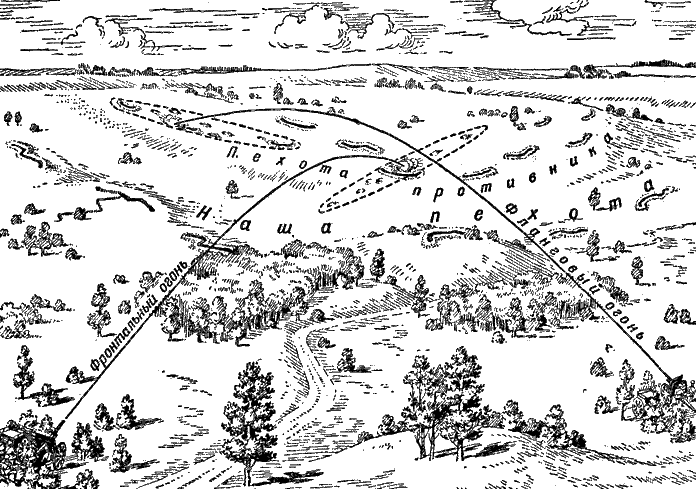
По той же причине, как видно из рисунка 202, фланговый огонь артиллерии наносит гораздо большее поражение вытянутым вдоль фронта войскам (окопам) противника, чем огонь фронтальный.
Кроме рассеивания по дальности и рассеивания по направлению имеется еще рассеивание по высоте. Иначе и не может быть: ведь снаряды летят не по одной и той же траектории, а расходящимся снопом.
Если бы мы поставили на пути летящих снарядов большой деревянный щит так, чтобы каждый летящий снаряд пробил в нем отверстие, то мы увидели бы, как происходит рассеивание по высоте (рис. 203).
Рис. 203. Рассеивание траекторий по высоте
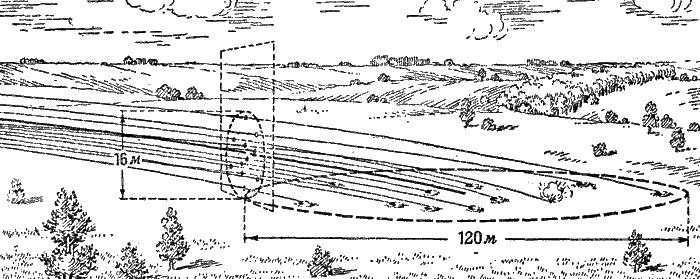
Вертикальная площадь рассеивания и по размерам, и по форме будет иная, чем площадь рассеивания на горизонте. Рассеивание по высоте обычно будет гораздо меньшим, чем рассеивание по дальности, и все более и более резко будет отличаться от него по мере приближения цели к орудию.
Например, при стрельбе гранатой из 76-миллиметровой дивизионной пушки на дальность 1 600 метров рассеивание по высоте равно лишь 16 метрам, а рассеивание по дальности в этом же случае равно примерно 120 метрам (рис. 203).
Небольшое рассеивание по высоте позволяет легко поражать такие цели, которые выдаются над поверхностью земли и находятся при этом сравнительно недалеко от орудия. В таких условиях, например, происходит часто стрельба по танкам.
Здесь меньше всего сказывается вредное влияние рассеивания.
