Цель найдена. Теперь нужно определить ее местоположение, нужно точно вычислить расстояние до цели, чтобы наша артиллерия знала, куда направить свои выстрелы.
Как же это сделать?
Местоположение цели определяется обычно по отношению к ориентиру, – именно, по отношению к тому ориентиру, который находится всего ближе к цели. Достаточно знать две координаты цели – ее дальность, то-есть расстояние от наблюдателя или от орудия до цели, и угол, на который цель видна нам правее или левее ориентира, – и тогда местоположение цели будет определено вполне точно.
Предположим, ради простоты, что цель находится от нас на том же расстоянии, что и ориентир. Расстояние до ориентира нам, конечно, известно заранее: мы потому и называем предмет ориентиром, что местоположение его нам уже известно. Пусть расстояние до ориентира равно 1000 метров. Одна координата цели, следовательно, уже определена. Остается определить другую: угол между целью и ориентиром, – насколько цель видна нам правее или левее ориентира.
Чем же и как артиллеристы измеряют углы? В обыденной жизни вам не раз приходилось измерять углы: вы измеряли их в градусах и минутах. Артиллеристам же приходится не только измерять углы, но и быстро в уме переводить полученные угловые величины в линейные и наоборот. Поэтому измерение углов градусами и минутами для артиллеристов неудобно.
Артиллеристы придумали совсем иную меру углов. Мера эта – «тысячная», или, как ее называют иначе, «деление угломера». Представьте себе окружность, разделенную на 6 000 равных частей. Примем за основную меру для измерения углов одну шеститысячную долю этой окружности и попробуем определить ее величину в долях радиуса.
Рис. 174. В артиллерии углы измеряют «тысячными»
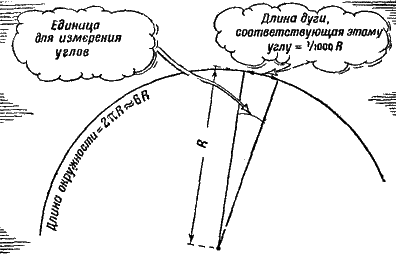
Длина любой окружности превосходит, как известно, длину ее радиуса приблизительно в шесть раз. Значит, одна шеститысячная часть окружности – та мера, которой мы решили измерять углы, – будет равна примерно одной тысячной радиуса окружности… Поэтому-то артиллерийская мера углов и носит название «тысячной» (рис. 174). Этой мерой измерять углы очень удобно. Вы убедитесь в этом сами на следующих двух примерах.
Пример первый (рис. 175). Вы определяете угол, под которым видны с вашего наблюдательного пункта пулемет противника и отдельно стоящая сосна. Угол этот равен, оказывается, ста «тысячным». И пулемет, и сосна расположены на одинаковом от вас расстоянии-на расстоянии 2000 метров. Вас интересует, поразят ли осколки 152-миллиметровой гранаты людей у пулемета, если граната разорвется около сосны. Для этого, очевидно, надо прежде всего знать, как же велико расстояние от сосны до пулемета, если его измерять не в угловых, а в линейных величинах, то-есть в метрах.
Рис. 175. Как по углу определить расстояние от цели до ориентира
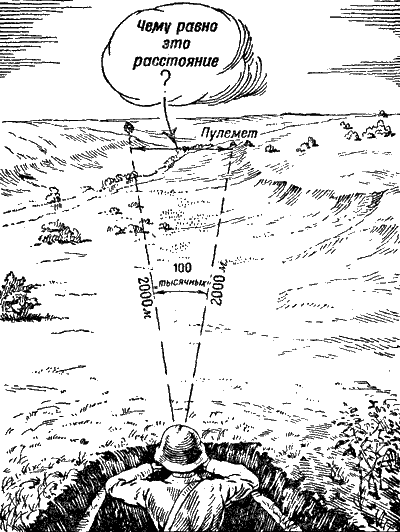
Задача эта решается очень просто. Надо только представить себе, что ваш наблюдательный пункт – это центр той окружности, которая описана радиусом, равным расстоянию от вас до пулемета (или до сосны). Радиус, таким образом, будет равен 2 000 метров. Углу в одну «тысячную» соответствует, как вы знаете, расстояние, равное одной тысячной радиуса, то-есть в данном случае 2 метрам. А так как угол между пулеметом и сосной равен не одной, а ста «тысячным», то, значит, расстояние между пулеметом и сосной равно не 2 метрам, а 200 метрам.
Мы знаем, что действительное поражение осколки 152-миллиметровой гранаты наносят на расстоянии до 35 метров от точки разрыва (рис. 73). Значит, в данном случае нельзя рассчитывать на поражение пулеметчиков осколками гранаты, рвущейся у сосны.
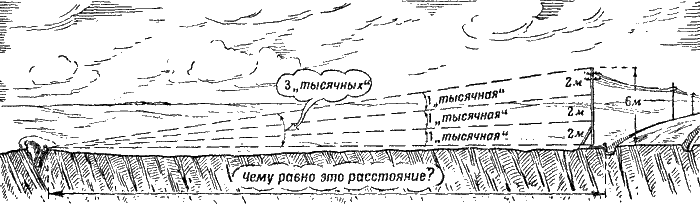
Еще один пример (рис. 176). В канаве около шоссе вы обнаружили группу стрелков, по которой и решили открыть огонь. Вам надо вычислить расстояние до стрелков или, что то же, до шоссе.
Для решения этой задачи воспользуйтесь телеграфными столбами на шоссе; высота их известна – она равна 6 метрам.
Измерьте теперь угол, которым покрывается высота телеграфного столба, и вы будете иметь все данные для решения этой задачи. Допустим, что угол этот оказался равным 3 «тысячным». Но если 6 метрам соответствует с этого расстояния угол в 3 «тысячных», то 1 «тысячной» будут соответствовать 2 метра. А всему радиусу, то-есть расстоянию от вас до шоссе, будет соответствовать величина, в 1 000 раз большая. Нетрудно сообразить, что расстояние от вас до шоссе будет равно 2 000 метров.
В действительности не все расстояния будут выражаться такими числами, как 2 000, 3 000 метров. Числа могут и не оканчиваться нулями. Но принятая в артиллерии мера для измерения углов позволяет, как в этом вы уже убедились, без всякого труда быстро находить одну «тысячную» от любого из таких чисел. Для этого надо только мысленно отделить в таком числе справа три знака, и вы получите значение одной «тысячной» этого числа. Все это проделывается очень быстро в уме.
Рис. 176. Как «тысячные» помогают определить дальность до цели
А вот что получилось бы, если бы вы за меру углов приняли не «тысячную», а обычную, применяемую в геометрии, меру углов: один градус или одну минуту. Угол в один градус был бы равен 1/60 радиуса, а угол в одну минуту 1/3600 радиуса, и, следовательно, при решении любой из приведенных задач вам приходилось бы делить числа, выражающие расстояние до целей, не на 1 000, а на 60 или на 3 600. Попробуйте проделать это деление с любым выбранным наугад числом, и вы сейчас же убедитесь, что без карандаша и бумаги вам здесь не обойтись.
Рис. 177. Сетка бинокля: маленькое деление равно пяти «тысячным», большое – десяти «тысячным»
Рис. 178. Такое приспособление имеется у стереотрубы: с его помощью измеряют углы с точностью до одной «тысячной»
Шкалы всех артиллерийских приборов приспособлены к измерению углов в «тысячных», или, иначе говоря, в делениях угломера.
Рис. 179. Ваши пальцы могут служить вам простейшим угломерным прибором
Рис. 180. «Цена» пальцев и кулака в «тысячных»
Рис. 181. «Цена» карандаша и спичечной коробки в «тысячных»
Вспомните, что в поле зрения бинокля вы всегда видели сетку с делениями (рис. 177). Эти деления и есть «тысячные». Самое маленькое деление сетки равно пяти, а большое – десяти «тысячным».
На рисунке 177 эти деления обозначены не просто числами «5» и «10», а с приставленными слева нолями – «0-05» и «0-10». Так пишут и произносят артиллеристы все величины в «тысячных», чтобы избежать ошибок в командах. Если нужно скомандовать, например, «правее 185 «тысячных», то произносят это число, как номер телефона: «один восемьдесят пять», а пишут 1-85.
Сетка с делениями, такая же, как в бинокле, имеется и в поле зрения стереотрубы. Но стереотруба имеет еще угломерную шкалу снаружи.
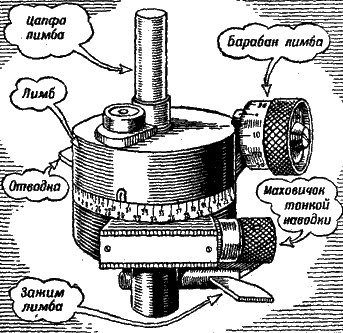
На рисунке 178 показаны те части стереотрубы (лимб и барабан лимба), с помощью которых можно производить более точно, чем по сетке, измерение горизонтальных углов.
Окружность лимба стереотрубы разделена на 60 частей, и поворот лимба на одно деление соответствует, таким образом, 100 «тысячным». Окружность же барабана лимба разделена на 100 частей, и полный оборот барабана заставляет передвинуться лимб трубы всего только на одно деление. Таким образом, деление барабана соответствует не 100 «тысячным», а всего одной «тысячной». Это позволяет уточнять показания лимба в сто раз и дает возможность стереотрубой измерять углы с точностью до одной «тысячной».
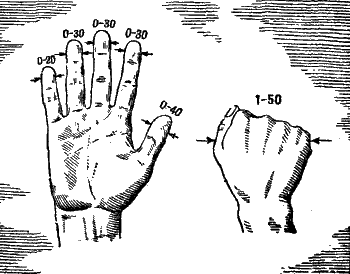
Но не только с помощью этих сложных приборов можно измерять углы. Ваша ладонь и ваши пальцы могут стать неплохим угломерным прибором, если только вы определите, сколько в них заключается «тысячных», какова «стоимость» их, или, как говорят артиллеристы, какова «цена» ладони и пальцев. Как это сделать, показано на рисунке 179.
Главное, о чем надо помнить при таком измерении, – это о вытягивании руки на полную ее длину.
Разные люди имеют разную длину руки и разную ширину пальцев. Поэтому каждый разведчик-наблюдатель должен заранее определить «цену» своей ладони, своих пальцев. «Цена» эта не будет сильно отличаться от указанной на рисунке 180.
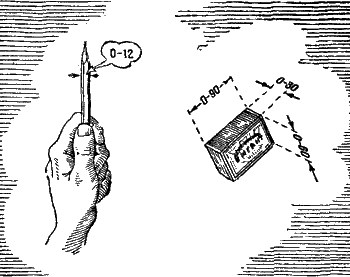
Понятно, что таким простейшим «угломером» может явиться всякий предмет, «цену» которого в «тысячных» вы заблаговременно определили. На рисунке 181 показаны такие предметы и их «цена» в «тысячных».
